A triangular number can be represented as a triangular grid of points, in which the first row contains one element and each succeeding row has one more element than the previous one. The first few triangular numbers are 1, 3, 6, 10, 15, and 21. If you include 0 as the first number, the nth triangular number is given by the formula n(n – 1)/2.

Triangular numbers depicted as triangular arrays of dots. Courtesy of Christian Boyer.
A magic square consists of a set of distinct integers arranged in the form of a square so that the numbers in each row, column, and diagonal all add up to the same total.
In 1941, the American Mathematical Monthly published the following problem, posed by Royal Vale Heath, widely known for creating ingenious mathematical puzzles: "What is the smallest value of n for which the n2 triangular numbers 0, 1, 3, 6, 10, . . . n2(n2 – 1)/2 can be arranged to form a magic square?"
At that time, the journal's "Problems and Solutions" section was edited by Otto Dunkel, Orrin Frink Jr., and H.S.M. Coxeter.
A year later, Heath himself proposed a partial solution. He noted that a magic square that is still magic after the original entries are all squared (a bimagic square) can itself be used directly to construct a magic square of triangular numbers. Heath wrote, "Clearly, the magic property will still be retained if each of the original numbers is subtracted from its square. The resulting numbers are all even, and their halves are the triangular numbers."
Starting with a known bimagic square of order 8 (an eight-by-eight array), Heath then constructed a magic square of 64 triangular numbers, from 0 to 2016, with magic sum of 5460. He admitted, however, that a smaller set of distinct triangular numbers might also form a magic square.
So, Heath's puzzle remained unsolved until it finally came to the attention of Christian Boyer, who has recently put a lot of time and effort into exploring magic squares. Boyer proved that magic squares of triangular numbers are impossible for orders 3, 4, and 5. He did, however, discover magic squares using 36 triangular numbers from 0 to 630 (with a magic sum equal to 1295).
Here's an example.
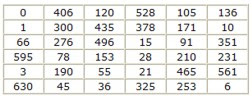
Boyer also found that there are magic squares of order 7, which use the first 49 triangular numbers, starting with 0. Furthermore, you can obtain magic squares of orders 6 and 7 when you start with 1 instead of 0.
What is the smallest order n possible if you allow the use of any triangular numbers rather than consecutive ones? Boyer has found the first four-by-four and five-by-five magic squares of distinct triangular numbers.
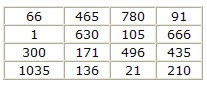
But it is still unknown whether a three-by-three magic square of distinct triangular numbers exists.
References:
Boyer, Christian. 2007. Better late than never (Solution to problem E 496). American Mathematical Monthly 114(October):745-746. Expanded version of this solution.
Heath, R.V. 1942. A magic square of triangular numbers (Solutions: E 496). American Mathematical Monthly 49(August-September):476.
______. 1941. Problems for solution: E 496. American Mathematical Monthly 48(December):699.
Peterson, I. 2005. Magic squares of squares. MAA Online (June 27).

No comments:
Post a Comment