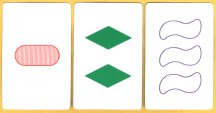
The card game known as SET® is deceptively simple. Its object is to identify, as quickly as possible, a grouping (SET) of three cards, selected from 12 cards laid out face up on a table.
A SET deck has 81 (34) cards. Each card displays a design with four attributes: shape, number, shading, and color. Each attribute has three possible values.
Attribute | Values |
Shape | {oval, diamond, squiggle} |
Number | {one, two, three} |
Shading | {striped, solid, open} |
Color | {red, green, purple} |
For the purposes of the game, three cards are called a SET if, with respect to each of the four attributes, the cards are either all the same or all different. For example, the following three cards would constitute a SET because the cards are different for all attributes.
Invented in 1974 by population geneticist Marsha Jean Falco, the game has become a popular, even addictive pastime for both children and adults. It has also attracted mathematical attention.
"Although children often beat adults, the game has a rich mathematical structure linking it to the combinatorics of finite affine and projective spaces and the theory of error-correcting codes," Diane Maclagan and Benjamin Lent Davis remarked in a paper published in the September 2003 Mathematical Intelligencer. In 2002, “an unexpected connection to Fourier analysis was used to settle a basic question directly related to the game of SET, and many related questions remain open."
The cards that make up SET have several important combinatorial properties. Given any two cards, there exists one and only one card that forms a set with those cards. Hence, the probability of producing a SET from three randomly drawn cards is 1/79. Overall, the deck has 1080 unique winning combinations.
One obvious mathematical question about the game concerns the number of cards that must be dealt to guarantee the presence of a SET.
Anyone who has played the game knows that 12 cards are sometimes not enough to find a SET. Indeed, the rules specify that, if no SET is found, three additional cards must be dealt for the game to continue. This is repeated until a SET makes an appearance.
One way to find out how many cards are needed is to do an exhaustive computer search of all the possible combinations. Such a search would reveal a collection of 20 cards that has no SET. Every collection of 21 cards contains a SET.
It's also possible to picture each card as a point in four-dimensional space, where each of a point's four coordinates assumes one of three possible values. Three cards form a SET if and only if the three associated points are all on the same straight line in this finite four-dimensional space.
In effect, Maclagan and Davis noted, players of SET are searching for lines contained in a subset of this finite affine space. They then defined a cap to be a subset of the space not containing any lines and asked the maximum possible size of a cap in the given space, which is equivalent to asking for the maximum number of cards that would have no SET among them.
Interestingly, this question was answered in a mathematical context in 1971, 3 years before SET was invented.
It's also possible to extend the problem in various ways. "Although SET cards are described by four attributes, from a mathematical perspective there is nothing sacred about the number four," Maclagan and Davis wrote. "We can play a three-attribute version of SET, for example, by playing only with the red cards. Or we can play a five-attribute version of set by using scratch-and-sniff SET cards with three different odors."
You can then ask how the size of the maximal cap, a, depends on the number of attributes (dimension, d). The answer for five dimensions was worked out some years ago, and the value for six dimensions isn't yet known exactly.
Dimension | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Maximal cap | 2 | 4 | 9 | 20 | 45 | 112 | ? |
There are many more possible generalizations. For example, you could add another color, shape, form of shading, and number to the cards. Such generalizations suggest a host of new mathematical questions.
SET cards can also be used for other pursuits in recreational mathematics. For example, you could look for SET magic squares. The idea is to arrange selected cards in a three-by-three array so that any line on the square yields a SET. In fact, you can start with any three cards, and there will always be a way to fill in the rest of the blanks to make a SET magic square.
In the meantime, you can visit the official SET website and try the SET daily puzzle to get yourself warmed up for deeper mathematical challenges.
Originally posted Aug. 25, 2003.
Updated July 28, 2010.
References:
Brink, D.V. 1997. The search for SET (June).
Davis, B.L., and D. Maclagan. 2003. The card game SET. Mathematical Intelligencer 25(No. 3):33-40.
Magliery, T. 1999. The SET® Home Page.
Zabrocki, M. 2001. The Joy of SET.